Cold molecules

Introduction

Control - total control - is the preoccupation of the experimental physicist. The atom is a good place to start in the struggle for control, and has recently been thoroughly domesticated in spite of its insubordinate tendency. Laser cooled atoms, too chilly to rebel, can easily be confined or pushed around by magnetic or optical forces. Through the service of the obedient atom, physicists have been able to create Bose-Einstein condensates, atom interferometers and atom lasers, and are learning how to build a quantum computer. Having mastered the atom, the next logical adversary is the molecule. We have started a new programme of research that aims to bring molecules under our control.

The experiment

We begin our experiment by creating beams of moderately cold molecules using the supersonic expansion technique. The molecules are caught up inside a gas which expands through a small nozzle from a region of high pressure to a region of low pressure. The molecules cool during the expansion, typically to a temperature around 1K. Their thermal energy is converted into kinetic energy directed away from the nozzle - so the molecules are cold, but are moving fast in the lab. The next step is to decelerate these fast-moving molecules to rest so that they can be trapped, manipulated and studied. We plan to do this using a new technique known as Stark deceleration. The technique exploits the change in energy that a molecule experiences when placed in an electric field. Suppose for example, that the energy of a particular quantum state of a particular molecule increases with increasing electric field (known as a weak field seeking state because, in this state, the molecule seeks the lowest electric field in order to minimize its energy). For such a molecule to move into a region of high electric field, it must climb a potential hill and therefore slows down. When the molecule leaves the region of high electric field it falls back down the potential hill and so regains its original speed. However, if the electric field is suddenely turned off just when the molecule reaches the top of the hill, the energy it lost in climbing the hill will not be regained, and the molecule will have slowed down. This is the principle of Stark deceleration. For typical electric fields obtainable in the lab, the amount of velocity lost in this process is small compared to the typical velocity of the beam. However, the process can be repeated over and over by manufacturing an electrode structure that produces a chain of regions of high electric field, and switching the electric fields at just the right times so that the molecules lose speed at every stage of this chain.

Progress

We have been working with the heavy polar molecule YbF, a molecule that we are also using in our laboratory to measure the electric dipole moment of the electron. We have built a supersonic source of YbF by ablating an Yb target into a fluorine-containing carrier gas. We typically produce beams with temperatures of 3K. We have tested a prototype Stark decelerator consisting of 12 deceleration stages in an alternating gradient arrangement. Each deceleration stage acts as a lens that focusses the molecules in one of the transverse directions but defocusses them in the other transverse direction. By alternating the focussing and defocussing directions of successive lenses, an overall focussing can be achieved in both transverse directions. This method, known as alternating gradient focussing, is commonly used in charged particle accelerators. Using the prototype, we were able to decelerate our YbF molecules, removing 7% of their kinetic energy.

Future

Having tested the prototype, we are now building a much longer decelerator, which will ultimately be capable of bringing the molecules to rest in the lab. At this point, we intend to couple them into a molecule trap, where they may be stored for many seconds. Trapped polar molecules may be used to measure the electric dipole moment of the electron, a search for physics beyond the standard model. By trapping chiral molecules, it should be possible to study the role of the weak interaction in the emergence of homochirality in biological molecules. Once we have trapped the molecules we hope to cool them further, bringing them into the ultracold regime. Ultracold polar molecules offer a new dimension in cold atom physics, primarily due to their long-range dipole-dipole interactions.

As part of our research into controlling beams of molecules, we have built an Alternating Gradient (AG) molecular guide. The guide confines the molecules in the transverse direction by use of the Stark effect, the interaction between the energy eigenstates of a system and a static electric field ( E ).

The ground-state of the molecules is lowered by the presence of the electric field, and so to confine them requires a maximum of E along the axis of the guide. However, a maximum of E in free space is prohibited by Maxwell's equations. Instead, we use an electrode geometry which creates a saddle point in E. The molecules are focussed in one transverse direction and defocused in the other. By alternating the focus and defocus directions the beam can be guided along the length of the electrode array. The guide behaves like a sequence of alternating focusing and defocusing lenses which, overall, maintains a collimated beam.

We have built a guide with a four-electrode geometry, as shown in fig. 1. The 1m long electrodes (nearest neighbour separation, 2mm) are charged to give the desired saddle-point field. By switching the polarity the saddle point can be rotated through p/2 to give alternating focusing (F) and defocusing (D) regions. The guide thus comprises a sequence of repeating F-D cells. By varying the switching timing, the length of the lenses can be varied, which affects the number of stable trajectories along the guide.

The electrode geometry was chosen to provide a strongly harmonic field variation; transverse confinement in the high-field Stark limit can be treated as that of a harmonic potential. Typical molecular trajectories calculated with this approximation are shown in figure 2.

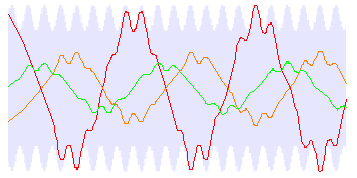
The form of the trajectory is a large-scale oscillation (‘macromotion') with a superimposed smaller-scale oscillation (‘micromotion'). The period of the micromotion is given by the length of one unit cell. The blue region shows the total transverse spatial extent that can be occupied by stable trajectories